Problem Description
Given a binary tree, determine if it is height-balanced.
A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
Example 1:
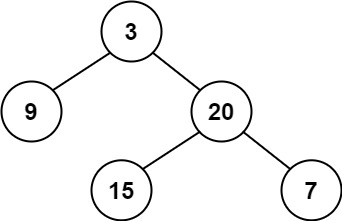
- Input:
root = [3,9,20,null,null,15,7] - Output:
True
Example 2:
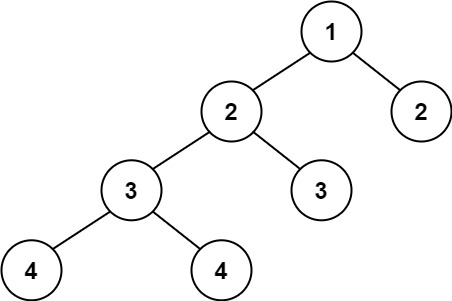
- Input:
root = [1,2,2,3,3,null,null,4,4] - Output:
False
Example 3:
- Input:
root = [] - Output:
True
My Idea
The idea here is very similar to the one in 543. Diameter Of Binary Tree. We will once again use a modified version of the maxDepth(root) function from 104. Maximum Depth Of Binary Tree to check for balance at every node, whilst only traversing the tree once. The result is once more stored in a list, so it can be modified from within the maxDepth(root, r) function. This leaves us with a time complexity of O(n).
My solution
from typing import Optional
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# Time Complexity: O(n)
def isBalanced(root: Optional[TreeNode]) -> bool:
res = [True]
def maxDepth(root,r):
if not root:
return 0
if not root.left and not root.right:
return 1
l = maxDepth(root.left,r)
r = maxDepth(root.right,r)
if l>r:
diff = l-r
else:
diff = r-l
if diff > 1:
res[0]=False
return 1 + max(l,r)
maxDepth(root,res)
return res[0]