Problem Description
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The length of a path between two nodes is represented by the number of edges between them.
Example 1:
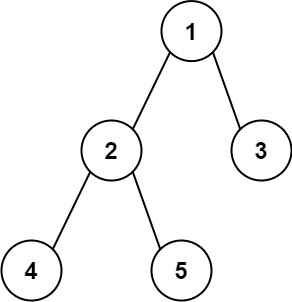
- Input:
root = [1,2,3,4,5] - Output:
3 - Explanation:
3 is the length of the path [4,2,1,3] or [5,2,1,3].
Example 2:
- Input:
root = [1,2] - Output:
1
My Idea
The idea here is to use a modified version of the maxDepth(root) function from 104. Maximum Depth Of Binary Tree. First we initialize our res variable as a list, since integers are immutable inside nested functions in python. Our modified maxDepth(root,d) function now takes an additional parameter, which is a reference to res. Furthermore instead of only calculating the max depth of a node, it also calculates the current max diameter at this node and updates the global res if needed. This way we work our way bottom-up and calculate the possible diameters whilst only doing a single traversal of the tree. This yields a time complexity of O(n).
My solution
from typing import Optional
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# Time Complexity: O(n)
def diameterOfBinaryTree(root: Optional[TreeNode]) -> int:
res = [0]
def maxDepth(root,d):
if not root:
return 0
if not root.left and not root.right:
return 1
l = maxDepth(root.left,d)
r = maxDepth(root.right,d)
res[0] = max(res[0], l+r)
return 1 + max(l,r)
maxDepth(root,res)
return res[0]