Problem Description
Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.
There is only one repeated number in nums, return this repeated number.
You must solve the problem without modifying the array nums and using only constant extra space.
Example 1:
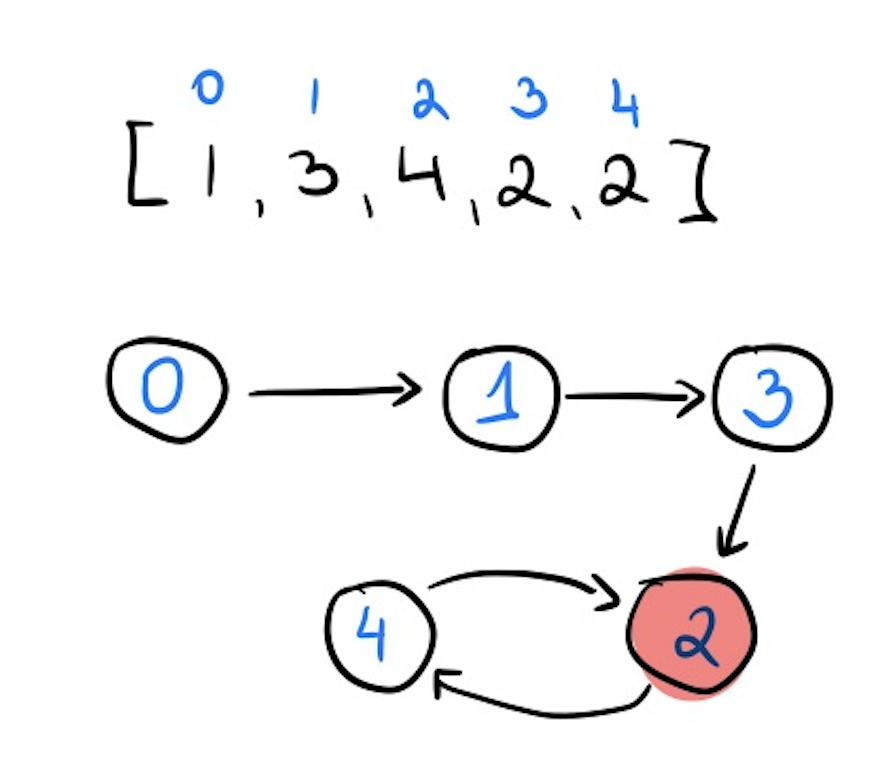
- Input:
nums = [1,3,4,2,2] - Output:
2
Example 2:
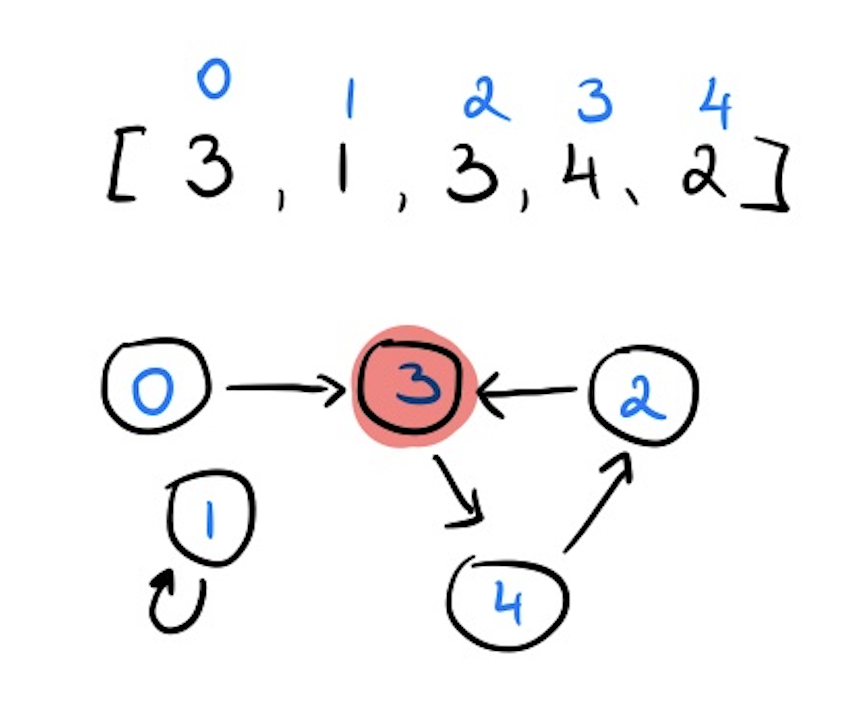
- Input:
nums = [3,1,3,4,2] - Output:
3
My Idea
The hard part here is figuring out that the array can be seen as a singly inked list, where the index is the value of the node and the value at this index is a pointer to the next node. This means that we can utilize Floyd’s algorithm like in 141. Linked List Cycle. In this case, however, we know for sure that we have a cycle, but are interested in the first node of the cycle, since this is the node that has multiple other nodes pointing at it, meaning that in our array representation there are multiple values that are equal. After the f and s pointers meet and confirm the presence of a loop, we create a second slow pointer s2 and move it one step at a time together with s. According to Floyd’s algorithm the two pointers meet at the node, which begins the cycle. By doing this we have not modified the array in any way and have used constant space O(1) and linear time O(n).
My solution
# Time Complexity: O(n)
def findDuplcate(nums:list[int]) -> int:
s = 0
f = 0
s = nums[s]
f = nums[nums[f]]
while(s!=f):
s = nums[s]
f = nums[nums[f]]
s2 = 0
s2 = nums[s2]
s = nums[s]
while(s!=s2):
s2 = nums[s2]
s = nums[s]
return s