Problem Description
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.
Return True if there is a cycle in the linked list. Otherwise, return False.
Example 1:
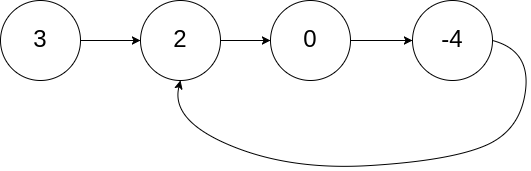
- Input:
head = [3,2,0,-4], pos = 1 - Output:
True - Explanation:
There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
Example 2:

- Input:
head = [1], pos = -1 - Output:
False
My Idea
My initial idea was to traverse the list, taking note of every visited element and returning True , if we encounter an already visited node. This, however, yielded a time complexity of O(n^2). Then I remembered there was a dedicated algorithm to solve this problem and after a quick search i remembered Floyd’s Cycle Detection Algorithm, where we create two pointers a slow one, which traverses the list 1 node at a time and a fast one, which does it two steps at a time. If there is a cycle in the list the fast pointer will eventually catch up with the slow one, otherwise it will reach the end. This approach brought the time complexity down to O(n).
My solution
from typing import Optional
# Definition for singly-linked list.
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
# Floyd’s Cycle Detection Algorithm
# Time Complexity: O(n)
def hasCycle(head: Optional[ListNode]) -> bool:
if not head:
return False
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if slow == fast:
return True
return False
# Time Complexity: O(n^2)
def hasCycleInitial(head: Optional[ListNode]) -> bool:
seen = []
if not head:
return False
curr = head
while curr:
if curr in seen:
return True
else:
seen.append(curr)
curr = curr.next
return False