Problem Description
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1:
- Input:
root = [1,2,3,null,5,null,4] - Output:
[1,3,4] - Expalantion:
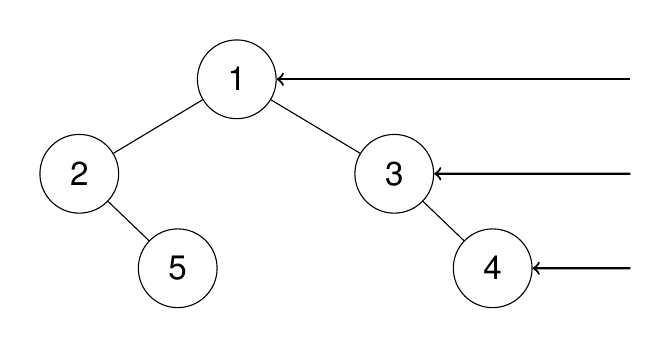
Example 2:
- Input:
[1,2,3,4,null,null,null,5] - Output:
[1,3,4,5] - Expalantion:
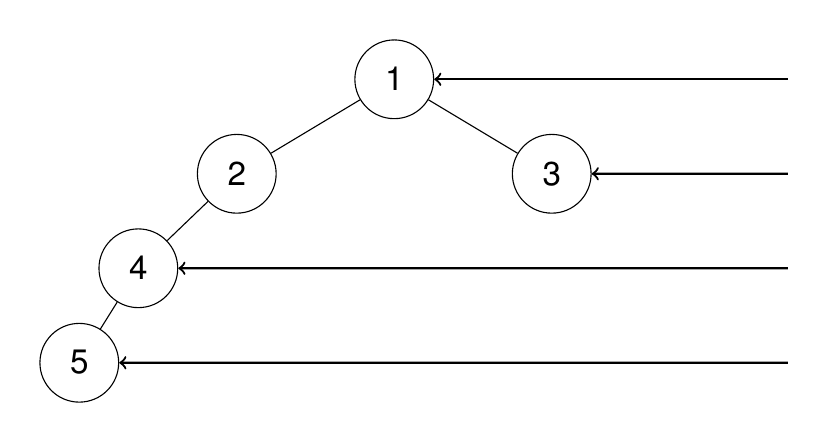
My Idea
The trick here is to see that what we need is essentially the rightmost element of every level. This means the last element of every level after a BFS, so we can simply modify the res.append() statement of the code from 102. Binary Tree Level Order Traversal to only add the last element for each level to res. This means we get the same time complexity of O(n).
My solution
from typing import Optional
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# Time Complexity: O(n)
from collections import deque
def rightSideView(root: Optional[TreeNode]) -> List[int]:
res = []
q = deque()
q.append(root)
while q:
lvl = []
l = len(q)
for _ in range(l):
curr = q.popleft()
if curr:
lvl.append(curr.val)
q.append(curr.left)
q.append(curr.right)
if lvl:
res.append(lvl[-1])
return res