85. Longest Rectangle in Histogram - Leet Code

Problem Description

Given an array of integers heights, representing the histogram’s bar height, where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

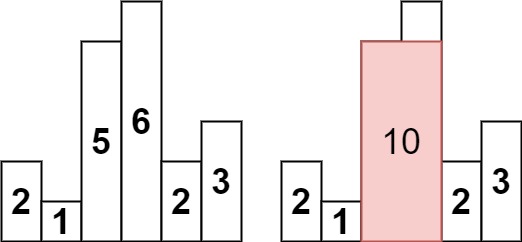
• Input: heights = [2,1,5,6,2,3]
• Output: 10
• Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

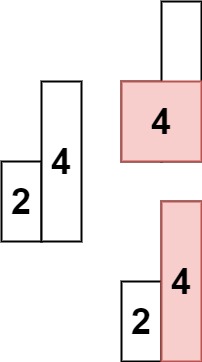
• Input: heights = [2,4]
• Output: 4

My Idea

Here we once more make use of a stack to keep track of the bars. In order not to have to consider items left in the stack we add a fictitious bar of height=0 to the end of heights. We iterate through the heights array adding a tuple (index,height) if the current height is >= the topmost one in the stack. Once we meet a height that is lower than the one in the stack this means that the bar at the top of the stack can’t form a rectangle with its height further to the right. Thus we pop it from the stack, calculating the highest rectangle of this hight possible and modifying the max_height variable accordingly. We do this until the topmost element of the stack is <= the current one. Then we add the current element to the stack, but keeping the index of the last popped element as the current index, since a rectangle of the current hight can be built starting at the index of the last popped bar.

My solution

# Time Complexity: O(n)
def largestRectangleArea(heights: list[int]) -> int:
    s=[]
    heights.append(0)
    max_area=0
    for i,h in enumerate(heights):
        if (s==[] or s[-1][1]<=h):
            s.append((i,h))
        else:
            while s[-1][1]>h:
                ci,ch=s.pop()
                max_area=max(max_area,(ch*(i-ci)))
                if s==[]:
                    break
            s.append((ci,h))
    return max_area