Problem Description

You are given an m x n integer matrix matrix with the following two properties:

Each row is sorted in non-decreasing order. The first integer of each row is greater than the last integer of the previous row. Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

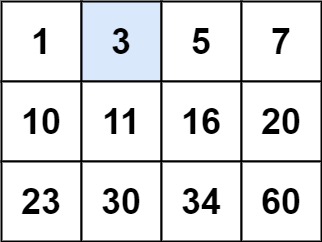
2DMatrix1.jpg

  • Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
  • Output: True

Example 2:

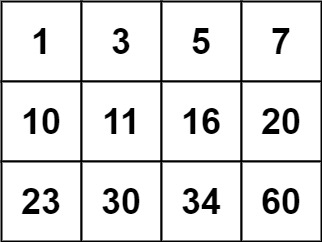
2DMatrix2.jpg

  • Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
  • Output: False

My Idea

My idea here was to first utilize binary search on the first element of each row to find the possible row for target and then do one more binary search within this row to check if target is indeed there, thus yielding the desired time complexity of O(log m*n).

My solution

# Time Complexity: O(log m*n)
def searchMatrix(matrix: list[list[int]], target: int) -> bool:
    top = 0
    bot = len(matrix)-1
    mid = (top+bot) // 2
    while(top<=bot):
        if matrix[mid][0]>target:
            bot = mid-1
            mid = (top+bot) // 2
        elif matrix[mid][0]<target:
            top = mid+1
            mid = (top+bot) // 2
        else:
            return True
    l = 0
    r = len(matrix[mid])-1
    while(l<=r):
        m = (l+r) // 2
        if matrix[mid][m]>target:
            r = m-1
        elif matrix[mid][m]<target:
            l = m+1
        else:
            return True
    return False