Problem Description
Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
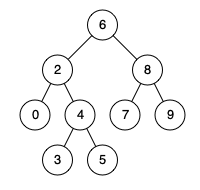
- Input:
root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 - Output:
6
Example 2:
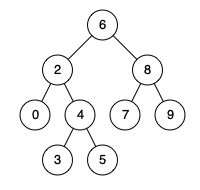
- Input:
root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 - Output:
2
My Idea
The idea here is to make use of the structure of a Binary Search Tree, namely that for each node the left subtree contains nodes with lower values and the right subtree contains nodes with higher values. This way we need to only check one node per level of the BST, which yields a time complexity of O(h), where h is the height of the tree.
My solution
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# Time Complexity: O(h), where h is the height of the tree
def lowestCommonAncestor(root: 'TreeNode', p: 'TreeNode', q:'TreeNode') -> 'TreeNode':
curr = root
while curr:
if curr.val > p.val and curr.val > q.val:
curr = curr.left
elif curr.val < p.val and curr.val < q.val:
curr = curr.right
else:
return curr