143. Reorder List - LeetCode

Problem Description

You are given the head of a singly linked-list. The list can be represented as:

$L_0 → L_1 → … → L_{(n - 1)} → L_n$

Reorder the list to be on the following form:

$L_0 → L_n → L_1 → L_{(n - 1)} → L_2 → L_{(n - 2)} → …$

You may not modify the values in the list’s nodes. Only nodes themselves may be changed.

Example 1:

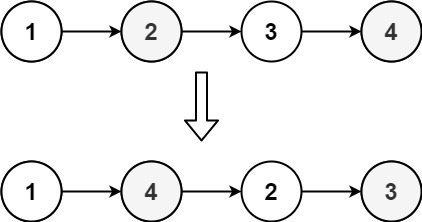
• Input: head = [1,2,3,4]
• Output: [1,4,2,3]

Example 2:

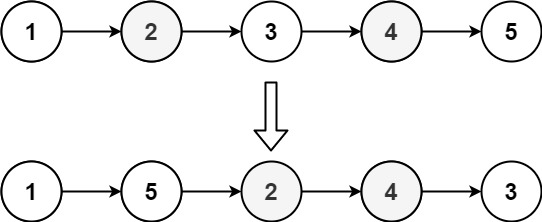
• Input: head = [1,2,3,4,5]
• Output: [1,5,2,4,3]

My Idea

One of the challenges here is to modify head in-place. This led me to the following approach: We separate the list in half by using two pointers a slow and a fast one, where the slow crawls 1 node at a time and the fast one 2. This means that if we have an even number of nodes once the fast one reaches the last element the slow one points at the last element from the first half. If we have an uneven number of nodes, once the fast one reaches the end, the slow one is pointing at the middle element, which for our purpose is also the last one from the first half. Then what we do is utilizing the logic from problem 206. Reverse Linked List we reverse the second half of the list. After which we merge the two halves. This yields a time complexity of O(n).

My solution

from typing import Optional
# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next
# Time Complexity: O(n)
def reoderList(head: Optional[ListNode]) -> None:
    # Do not return anything, modify head in-place instead!
    l = head
    # Separate the list in two halves
    r = head
    f = head.next
    while f and f.next:
        r = r.next
        f = f.next.next
    tmp = r.next
    r.next = None
    r = tmp
    # Reverse second half
    prev = None
    curr = r
    while curr:
        next = curr.next
        curr.next = prev
        prev = curr
        curr = next
    r = prev
    # Merge both halves
    while l and r:
        tl = l.next
        tr = r.next
        l.next = r
        l.next.next=tl
        r = tr
        l = l.next.next